Paper Summary: ResNet

ResNets created major improvements in accuracy in many computer vision tasks. Deep Residual Learning for image recognition was published in 2015.

Problem

Adding more layers leads to the model’s accuracy saturating, then rapidly decaying, and higher training errors — the degradation problem.

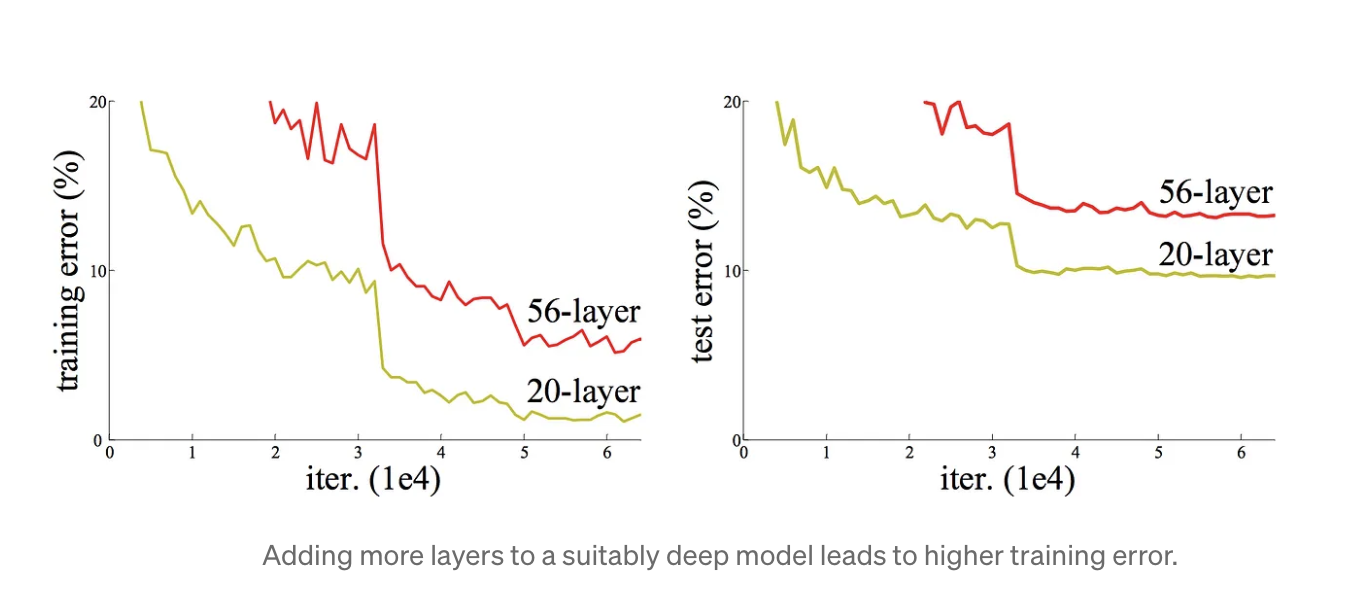Driven by the significance of network depth, a question arose: Is learning better networks as easy as stacking more layers? An obstacle to this question was the vanishing/exploding gradients problem.

The degradation of the training accuracy indicates that not all systems are similarly easy to optimize. Considering a shallower architecture and its deeper counterpart that adds more layers onto it: the added layers are identity mapping and the other layers are copied from the learned shallower model. therefore, a deeper model should produce no higher training error than its shallower counterpart.

Solution: Deep residual learning framework

Instead of hoping every few stacked layers directly fit a desired underlying mapping, we explicitly let these layers fit a residual mapping.

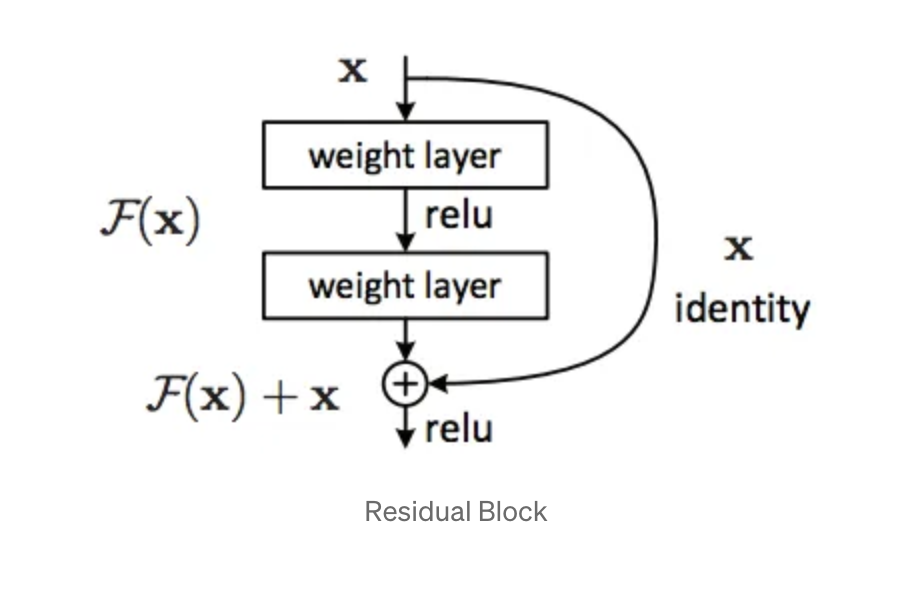
If H(x) is the underlying mapping of data to be fit by a few layers, then normally these layers try to learn a function F(x) that equals H(x), with x denoting the input to the network.

In ResNets, layers learn a residual function, F(x) = H(x) — x. Then x is added to the result afterwards, this is known as a shortcut connection. If the dimensions of x and F(x) are not equal e.g when changing the input/output channels, then a linear projection can be added to match their dimensions.

The identity shortcut can be directly used when the input and output are of the same dimension. when dimensions increase: (A) The shortcut still performs identity mapping, with extra zero entries padded for increasing dimension; (B) The projection shortcut is used to match dimensions (done by 1x1 convolutions).

The author’s hypothesis is that it is easy to optimize the residual mapping function F(x) than to optimize the original, unreferenced mapping H(x).

x = number of inputs

H(x) = mapping function from input to output,
             normally H(x) would be learned

F(x) = residual function

proposed: F(x) = H(x) — x

F(x ) is learned and H(x) is recovered by adding x

Evaluation

plain and residual net CNN of 18 and 34 layers were trained.

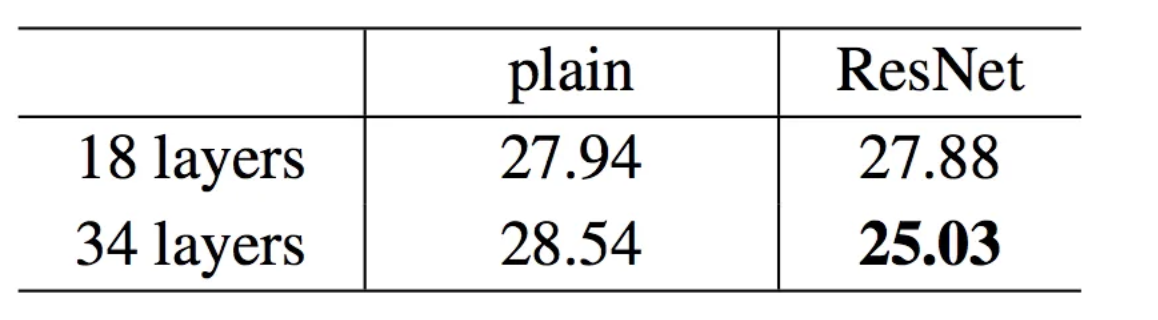
In plain CNN the error increases for plain networks when depth is increased from 18 to 34 layer while it reduces in ResNet with an increase in depth and the error was lower compared to plain nets.

The main contribution of this paper

Residual learning eases optimization. Solved the degradation problem. Faster training of deep neural networks. Decreases the error rate for deeper networks.

Real-world application of this contribution

It led to major improvements in Image recognition, image detection, image localization, and segmentation tasks. It contributed heavily to industrial applications such as medical image analysis, satellite image processing, and robot vision.

This architecture has more layers but lesser parameters than previous models hence making it fast.

Here is a pytorch implementation of ResNet.

References

[1] K. He, X. Zhang, S. Ren, and J. Sun, “Deep Residual Learning for Image Recognition,” 2015.

Back to learning!